Answer:
4 : 2√6 : √3 + 1
Explanation:
Our equation is:
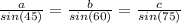
These are a few trig identities that we want to memorize:
- sin(45) = √2/2
- sin(60) = √3/2
- sin(75) = sin(45 + 30) = sin(45) * cos(30) + sin(30) * cos(45) = (√2/2)(√3/2) + (1/2)(√2/2) = √6/4 + √2/4 = (√6 + √2)/4
Put these in:
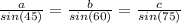

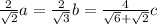
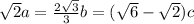
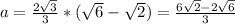
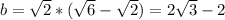

Then the ratio of a:b:c is:
(6√2 - 2√6) : (6√3 - 6) : (2√6), which simplifies to:
4 : 2√6 : √3 + 1
If you wanted, you could use a calculator to find the decimal form of that.