Answer:
f = 409 Hz
Step-by-step explanation:
We have,
Length of the open organ pipe, l = 0.29 m
Frequency of vibration of second overtone,
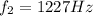
It is required to find the fundamental frequency of the pipe. For the open organ pipe, the frequency of second overtone is given by :
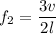
v is speed of sound
Let f is the fundamental frequency. It is given by :

The relation between f and f₂ can be written as :
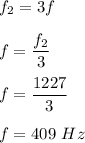
So, the fundamental frequency of the pipe is 409 Hz.