Question

100 POINTS

What is the average rate of change of the function over the interval x = 0 to x = 8?

f(x)=2x−1/3x+5
Enter your answer, as a fraction, in the box.

Answer 1

Explanation:

Step 1: Find the average rate of change

`ARC = (f(b)-f(a))/(b-a)`

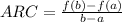
Average Rate of Change is same as ARC

If you mean:
`f(x)=2x - (1)/(3)x+5`

`ARC = (f(8)-f(0))/(8-0)`

`ARC=((2(8)-1/3(8)+5) - (2(0)-1/3(0)+5))/(8)`

`ARC=((16-8/3+5)-(5))/(8)`

`ARC=(16-8/3)/(8)`

`ARC=(40/3)/(8)`

`ARC=(5)/(3)`

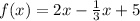
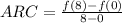
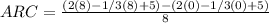
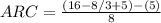
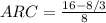
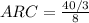
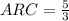
If by the first way, the answer is: The average rate of change is 5/3

If you mean:
`f(x)=(2x - 1)/(3x+5)`

`ARC=(f(8)-f(0))/(8-0)`

`ARC=((2(8)-1)/(3(8)+5)-(2(0)-1)/(3(0)+5) )/(8)`

`ARC=( (15)/(29) - (-1)/(5) )/(8)`

`ARC=(( 104 )/( 145 ) )/(8)`

`ARC=( 13 )/( 145 )`

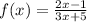
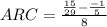
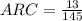
If by the second way, the answer is: The average rate of change is 5/3