Answer:
The required simplified base would be 3∛4
Explanation:
Given exponential function that:
![f(x)=(1)/(4)(\sqrt[3]{108})^x](https://img.qammunity.org/2021/formulas/mathematics/middle-school/xeks027h869f79nedoolxhcs0g7ixwi58a.png)
As we can see, 108 is the base of the exponential function with the form:
f(x) = a
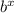
So, we can factor 108 = 2 × 2 × 3 × 3 × 3
<=> 108 = 4 × 3³
Hence,
![\sqrt[3]{108} = \sqrt[3]{4* 3^3}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/lif25g78nia1tj53x12wsbz7px96wp9qdt.png)
So we have:
![\sqrt[3]{108}=\sqrt[3]{4}* \sqrt[3](3^3)](https://img.qammunity.org/2021/formulas/mathematics/middle-school/o2kvj50qd7w2jo0xvzoylcr6hteenvm5t5.png)
<=>
![\sqrt[3]{108}=\sqrt[3]{4}* (3^3)^(1)/(3)](https://img.qammunity.org/2021/formulas/mathematics/middle-school/n8z9xew89dee8kzxfpzdilu6ircoenj54s.png)
<=>
![\sqrt[3]{108}=\sqrt[3]{4}* 3^{3* (1)/(3)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/nuf9ydlh2m6iotxli8n3mhy6ovvt5ubtrw.png)
<=>
![\sqrt[3]{108}=3\sqrt[3]{4}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/3kjf4qdyffkqpfsdjvzhnbof4344jan6na.png)
Hence, the required simplified base would be 3∛4