Question

What is the simplified base of the function f(x) = One-fourth (Root Index 3 StartRoot 108 EndRoot) Superscript x?

3
3RootIndex 3 StartRoot 4 EndRoot
6RootIndex 3 StartRoot 3 EndRoot
27

Answer 1

B.

Explanation:

Answer 2

The required simplified base would be 3∛4

Explanation:

Given exponential function that:

`f(x)=(1)/(4)(\sqrt[3]{108})^x`

As we can see, 108 is the base of the exponential function with the form:

f(x) = a
`b^(x)`

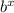
So, we can factor 108 = 2 × 2 × 3 × 3 × 3

<=> 108 = 4 × 3³

Hence,
`\sqrt[3]{108} = \sqrt[3]{4* 3^3}`

So we have:

`\sqrt[3]{108}=\sqrt[3]{4}* \sqrt[3](3^3)`

<=>
`\sqrt[3]{108}=\sqrt[3]{4}* (3^3)^(1)/(3)`

<=>
`\sqrt[3]{108}=\sqrt[3]{4}* 3^{3* (1)/(3)}`

<=>
`\sqrt[3]{108}=3\sqrt[3]{4}`

Hence, the required simplified base would be 3∛4