Answer:
The revenue function is
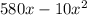
The marginal revenue function is
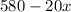
Explanation:
We have
 where
where
 is the number of cakes sold per day and
is the number of cakes sold per day and
 is the price.
is the price.
Also, we have
 where
where
 is also the number of cakes and
is also the number of cakes and
 is the total cost.
is the total cost.
The revenue would be

The marginal revenue would be the derivative of the revenue function
![(d)/(dx)[580x-10x^(2) ] =580-20x](https://img.qammunity.org/2021/formulas/mathematics/college/bzjt4791b7i8xypchxu4r4fngg3503ccbk.png)
Therefore, the answers are
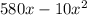 and
and
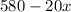 , respectively.
, respectively.