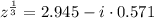Question

Find the cube roots of 27(cos 327° + i sin 327° ). Write the answer in trigonometric form.

Answer 1

`z^{(1)/(3) }= -0.978 + i\cdot 2.836`,
`z^{(1)/(3) }= -1.967 - i\cdot 2.265`,
`z^{(1)/(3) }= 2.945 - i\cdot 0.571`

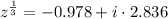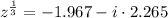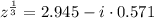
Step-by-step explanation:

The cube root of the complex number can determined by the following De Moivre's Formula:

`z^{(1)/(n) } = r^{(1)/(n) }\cdot \left[\cos\left((x + 2\pi\cdot k)/(n) \right) + i\cdot \sin\left((x+2\pi\cdot k)/(n) \right)\right]`

Where angles are measured in radians and k represents an integer between
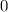`0` and
`n - 1`.

The magnitude of the complex number is
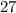`27` and the equivalent angular value is
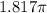`1.817\pi`. The set of cubic roots are, respectively:

k = 0

`z^{(1)/(3) } = 3\cdot \left[\cos \left((1.817\pi)/(3) \right)+i\cdot \sin\left((1.817\pi)/(3) \right)]`

`z^{(1)/(3) }= -0.978 + i\cdot 2.836`

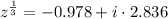
k = 1

`z^{(1)/(3) } = 3\cdot \left[\cos \left((3.817\pi)/(3) \right)+i\cdot \sin\left((3.817\pi)/(3) \right)]`

`z^{(1)/(3) }= -1.967 - i\cdot 2.265`

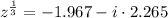
k = 2

`z^{(1)/(3) } = 3\cdot \left[\cos \left((5.817\pi)/(3) \right)+i\cdot \sin\left((5.817\pi)/(3) \right)]`

`z^{(1)/(3) }= 2.945 - i\cdot 0.571`