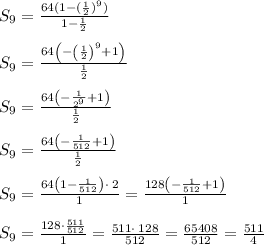Answer:
The sum of the first 9 terms is
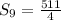 .
.
Explanation:
To find the sum of the first
 terms of a geometric sequence use the formula
terms of a geometric sequence use the formula
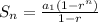
where,
 is the number of terms,
is the number of terms,
 is the first term and
is the first term and
 is the common ratio.
is the common ratio.
To find the common ratio, find the ratio between a term and the term preceding it.
Given the geometric sequence
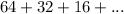 , the common ratio is
, the common ratio is
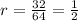
and the sum of the first 9 terms is