Angle A is circumscribed about circle O what is the length of AB

Question

asked Oct 8, 2021 226k views

1 Answer

Amanpreet · Answer 1 · 2021-10-15T04:32:32+0000

Answer:

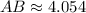
$AB \approx 4.054$

Explanation:

The trigonometric equations associated with the figure are, respectively:

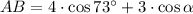
$AB = 4\cdot \cos 73^(\circ) + 3\cdot \cos \alpha$

$4\cdot \sin 73^(\circ) = 3 +3\cdot \sin \alpha$

The components with the unknown angle are cleared and used in the fundamental trigonometric relation:

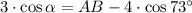
$3\cdot \cos \alpha = AB - 4\cdot \cos 73^(\circ)$

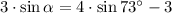
$3\cdot \sin \alpha = 4\cdot \sin 73^(\circ) - 3$

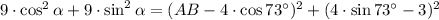
$9\cdot \cos^(2)\alpha + 9\cdot \sin^(2)\alpha =(AB-4\cdot \cos 73^(\circ))^(2)+(4\cdot \sin 73^(\circ)-3)^(2)$

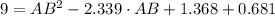
$9 = AB^(2)-2.339\cdot AB + 1.368 + 0.681$

The following second-order polynomial is presented below:

$AB^(2)-2.339\cdot AB -6.951 = 0$

Roots of the polynomial are described hereafter:

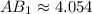$AB_(1) \approx 4.054$ and
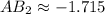
$AB_(2) \approx -1.715$

Only the first root is reasonable, as length is a positive variable. The length is
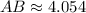$AB \approx 4.054$ .