Answer:
Explanation:
In the question we are given ,
- Side length ( Perpendicular ) = 60 cm
And we have asked to find the length of base that is denoted by x .
Solution : -
According to Pythagoras Theorem ,
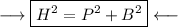
Where ,
Now , substituting value of hypotenuse, perpendicular and base :
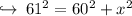
Now by squaring 61 and 60 , we get :
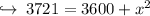
Now transposing 3600 to left hand side :
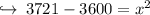
Now subtracting 3600 from 3721 :
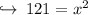
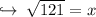
We know that 11 × 11 is equal to 121 that means square root of 121 is 11 . So :
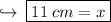
- Henceforth, length of base of right triangle is 11 cm .
#Keep Learning