Question

The figure shows a circle with center P and inscribed isosceles Triangle ABC. If AC has the same length as the radius of the circle, what is the measure of angle ABC

Answer 1

Answer: 30

it is because I got it right

Answer 2

<ABC =
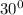`30^(0)` (The central angle of a circle is twice any inscribed angle subtended by the same arc).

Explanation:

From the diagram, ABC is an inscribed isosceles triangle. But the radius of the circle equals the length AC.

Join P to A and C to form an equilateral triangle. An equilateral triangle has equal sides and angles. So, the value of each interior angle of the equilateral triangle is;

Sum of angle in a triangle =
`180^(0)`

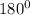
So that each interior angle =
`(180^(0) )/(3)`

=
`60^(0)`

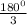
The value of each interior angle of the triangle is
`60^(0)`. Thus, <APC =
`60^(0)`.

⇒ <ABC =
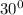`30^(0)` (The central angle of a circle is twice any inscribed angle subtended by the same arc.)