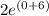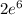When you have a negative exponent, you move the base with the negative exponent to the other side of the fraction to make the exponent positive.
For example:
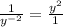 or
or
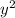
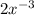 or
or
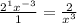
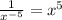
When a base with an exponent is divided by a base with an exponent, you subtract the exponents together. (But you can only combine the exponents when the bases are the same)
For example:
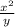 (can't combine because they have different bases of y and x)
(can't combine because they have different bases of y and x)
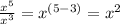
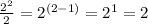
When you multiply an exponent directly to a base with an exponent, you multiply the exponents together.
For example:
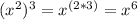
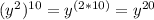
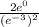 First multiply the exponents together in the denominator
First multiply the exponents together in the denominator
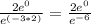 Now subtract the exponents together
Now subtract the exponents together
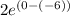 (two negative signs cancel each other out and become positive)
(two negative signs cancel each other out and become positive)