Answer:
(a) 74.12633 mm ≤ μ ≤ 74.12767 mm
(b) μ ≥ 74.12649 mm
Explanation:
Here we have;
Sample count, n = 15
Mean,
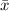 = 74.127 mm
= 74.127 mm
Standard deviation, σ = 0.001 mm
(a) The confidence interval, CI is given as follows;
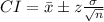
At 99%, z = ±2.575829
Therefore, the confidence interval is;
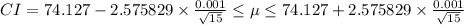
74.12633 mm ≤ μ ≤ 74.12767 mm
(b) The lower confidence at 95% is given by;
z at 95% = 1.959964
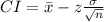
or μ ≥ 74.12649 mm.