Question

A manufacturer produces piston rings for an automobile engine. It is known that ring diameter is normally distributed with millimeters. A random sample of 15 rings has a mean diameter of x Overscript bar EndScripts equals 74.127. Construct a 99% two-sided confidence interval on the true mean piston diameter and a 95% lower confidence bound on the true mean piston diameter. (b) Calculate the 95% one-sided lower confidence interval on the true mean piston diameter.

Answer 1

(a) 74.12633 mm ≤ μ ≤ 74.12767 mm

(b) μ ≥ 74.12649 mm

Explanation:

Here we have;

Sample count, n = 15

Mean,
`\bar x` = 74.127 mm

Standard deviation, σ = 0.001 mm

(a) The confidence interval, CI is given as follows;

`CI=\bar{x}\pm z(\sigma)/(√(n))`

At 99%, z = ±2.575829

Therefore, the confidence interval is;

`CI=74.127 - 2.575829 * (0.001)/(√(15)) \leq \mu \leq 74.127 + 2.575829 * (0.001)/(√(15))`

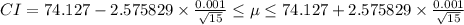
74.12633 mm ≤ μ ≤ 74.12767 mm

(b) The lower confidence at 95% is given by;

z at 95% = 1.959964

`CI=\bar{x} - z(\sigma)/(√(n))`

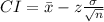
or μ ≥ 74.12649 mm.