Answer:
(a) The median is 1478
(b) Null hypothesis H₀ : μ₁ = μ₂
Alternative hypothesis Hₐ : μ₁ > μ₂
(c) The test statistic
 is 6.678155
is 6.678155
(d) The p value is 1.2×10⁻¹¹
(e) We reject our null hypothesis H₀. In terms of the test, there is sufficient evidence to suggest that there is a trend in the numbers of daily newspaper because the probability for a decrease in the numbers is very high
Explanation:
(a) Here we have the data as follows;
1623 1586 1574 1554 1544 1531 1519 1513 1491 1484 1478 1471 1458 1456 1458 1453 1438 1428 1405 1395 1377
The median is = 1478
Therefore we have above the median
1623 1586 1574 1554 1544 1531 1519 1513 1491 1484
The mean,
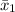 = 1541.9
= 1541.9
Standard deviation, σ₁ = 41.38224257
n₁ = 10
Below the median
1471 1458 1456 1458 1453 1438 1428 1405 1395 1377
The mean,
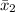 = 1433.9
= 1433.9
Standard deviation, σ₂ = 30.04812806
n₂ = 10
(b) Null hypothesis H₀ : μ₁ = μ₂
Alternative hypothesis Hₐ : μ₁ > μ₂
(c) The formula for t test is given by;
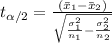
df = 10 - 1 = 9, α = 0.05
Therefore, the test statistic
 = 6.678155
= 6.678155
(d) The p value from statistical relations is Probability p = 1.2×10⁻¹¹
Critical z at 5% confidence level = 1.645
Since P << 0.05, e reject the
(e) Therefore, we reject our null hypothesis H₀. In terms of the test, there is sufficient evidence to suggest that there is a trend in the numbers of daily newspaper because the probability for a decrease in the numbers is very high.