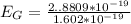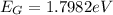Answer:
The energy gap of the material is
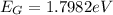
Step-by-step explanation:
From the question we are told that
The wavelength is

The band gap of the material can be mathematically represented as
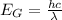
Where h is the Planck constant with value
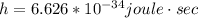
c is the speed of light with a value
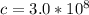
Substituting value
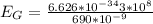
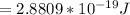
Now converting to eV we divide by the charge on on electron. the value is

so