Answer:
Final velocities are:
Wedge B: v = 2.334 m/s
Sphere A: v = 5.386 m/s
Step-by-step explanation:
Given:-
- The mass of sphere A, mA = 2-kg
- The mass of the wedge B, mB = 6-kg
- The sphere collides with " normal " to the wedge face.
- The coefficient of restitution , e = 0.5
- The wedge inclination angle, θ=40 degrees with the horizontal.
- The initial speed of sphere A, vA = 4m/s
- The initial speed of wedge B, vB = 0 m/s ... ( rest )
Find:-
- First step would be to sketch a system of sphere A and wedge B as ( FBD ).
- We will add a sketch of "two" coordinate axes on the ( FBD ).
First coordinate system ( normal ( n ) - tangent ( t ) )
- Normal axis at 90 degrees directed towards the wedge in direction of sphere motion - denote as ( n ).
- Tangent axis along ( parallel ) to the wedge surface directed up the wedge - denote as ( t )
Second coordinate system ( horizontal ( x ) - vertical ( y ) )
- Horizontal axis parallel to ground directed towards the right in assumed direction of wedge motion after impact - denote as ( x ).
- Vertical axis normal to the ground directed upwards -denote ( y ).
Note:- All the above directions of coordinate axes denote the positive direction of vectors.
- Resolve the angle ( α ) between the normal - ( n ) or velocity vector vA and the horizontal - ( x ) axis.
α = 90° - θ = 90° - 40°
α = 50°
- We will denote the final velocity components of sphere A as ( v'An , v'At ):
And, final velocity components of wedge B as ( v'B ).
- Transform the the final velocity of wedge ( vB' ) in the (n-t) coordinate axis using the resolved coordinate transformation angle ( α ). The normal ( n ) and tangential components of the velocity vector ( vB' ) are: ( vB'n , vB't ).
vB'n = vB'*cos ( α ) vB't = vB'*sin ( α° )
vB'n = vB'*cos ( 50° ) vB't = vB'*sin ( 50° )
- Note: There is no y-component of velocity of wedge. This is because the motion of wedge in the vertical direction is restricted by the ground - equilibrium conditions. Hence, v'By = 0.
- Consider the system of sphere A and wedge B to be isolated with no external forces acting on the system. For such conditions the principle of conservation of momentum ( P ) is valid. Which states:
PA,i + PBi = PA,f + PB,f
Where,
PA,i : The initial momentum of the sphere A
PB,i : The initial momentum of wedge B
PA,f : The final momentum of the sphere A
PB,f : The final momentum of wedge B.
- Using the data given and relations computed in the ( n-t ) coordinate system. We will use the principle of conservation of linear momentum in both axis ( n and t ) combined in vector momentum of system.
Conservation of linear momentum:
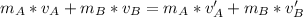
- Using vector notations we have, Taking ( i unit vector in tangential direction and j unit vector in the normal direction ):
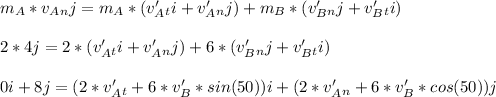
- Equate all the ( i - j ) vectors on left and right hand side of the equation respectively,
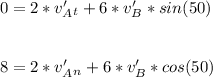 .... Eq 1
.... Eq 1
- The coefficient of restitution ( e ) is a squared loss of kinetic energy of the system that can be expressed in terms of velocities of two objects as relative change in velocity of two objects after and before impact.:
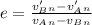
Note: We have only used the velocities normal to the surface of wedge. This is because the kinetic loss is a scalar dimension; hence, the normal direction to the surface of impact is assumed to cater all the loss in kinetic energy.
We have,
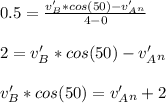 ..... Eq 2
..... Eq 2
- Now substitute equation 2 into equation 1:
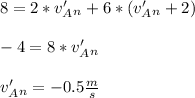
- Using Equation 2 compute v'B:
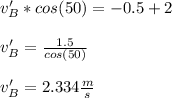
- Using Equation 1 compute v'At:
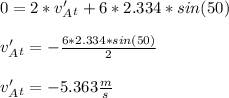
- The final velocity of wedge B along the horizontal direction ( x ) is:
vB' = 2.334 m/s .... x-direction
- The velocity of sphere A after impact is given by:
