Answer:
229.23 feet.
Explanation:
The pictorial representation of the problem is attached herewith.
Our goal is to determine the height, h of the tree in the right triangle given.
In Triangle BOH

Similarly, In Triangle BOL
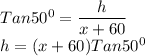
Equating the Value of h
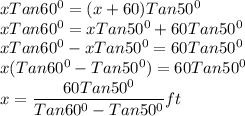
Since we have found the value of x, we can now determine the height, h of the tree.
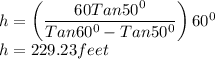
The height of the tree is 229.23 feet.