Question

Pat needs to determine the height of a tree before cutting it down to be sure that it will not fall on a nearby fence. The angle of elevation of the tree from one position on a flat path from the tree is Upper H equals 60 degrees comma and from a second position Upper L equals 60 feet farther along this path it is Upper B equals 50 degrees . What is the height of the​ tree?

Answer 1

229.23 feet.

Explanation:

The pictorial representation of the problem is attached herewith.

Our goal is to determine the height, h of the tree in the right triangle given.

In Triangle BOH

`Tan 60^0=(h)/(x)\\h=xTan 60^0`

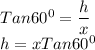
Similarly, In Triangle BOL

`Tan 50^0=(h)/(x+60)\\h=(x+60)Tan 50^0`

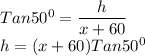
Equating the Value of h

`xTan 60^0=(x+60)Tan 50^0\\xTan 60^0=xTan 50^0+60Tan 50^0\\xTan 60^0-xTan 50^0=60Tan 50^0\\x(Tan 60^0-Tan 50^0)=60Tan 50^0\\x=(60Tan 50^0)/(Tan 60^0-Tan 50^0) ft`

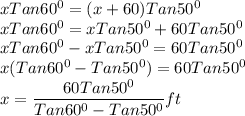
Since we have found the value of x, we can now determine the height, h of the tree.

`h=\left((60Tan 50^0)/(Tan 60^0-Tan 50^0)\right)\cdotTan 60^0\\h=229.23 feet`

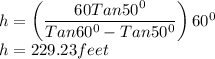
The height of the tree is 229.23 feet.