Answer:
The probability that when 11 adults are randomly selected, 3 or fewer are in excellent health is 0.6483.
Explanation:
The random variable X can be defined as the number of adults questioned reported that their health was excellent.
A random sample of n = 11 adults are selected randomly selected from an area a nuclear power plant.
Of these 11 adults X = 3 reported that their health was excellent.
The proportion of adults who reported that their health was excellent is:
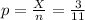
An adult's health condition is not affected by others, i.e. they are independent.
The random variable X follows a Binomial distribution with parameters n = 11 and p =
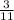 .
.
The probability mass function of X is:
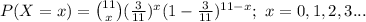
Compute the probability that when 11 adults are randomly selected, 3 or fewer are in excellent health as follows:
P (X ≤ 3) = P (X = 0) + P (X = 1) + P (X = 2) + P (X = 3)
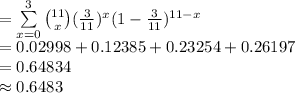
Thus, the probability that when 11 adults are randomly selected, 3 or fewer are in excellent health is 0.6483.