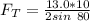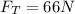Question

Problem: A uniform rod of mass M = 13.0 kg and length L = 1.80 m is held horizontally with one end anchored in the wall by a hinge that allows the rod to rotate freely in the x-y plane. The other end of the rod is attached to the wall with cable that makes angle θ = 80◦ with the rod. Magnitude of acceleration due to gravity is g = 10 m/s2. What is the magnitude of tension force FT in the cable?

Answer 1

The magnitude of the tension force is
`F_T = 66 N`

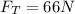
Step-by-step explanation:

The diagram of the question is shown on the first uploaded image

From the question we are told that

The mass of the rod is
`M = 13.0kg`

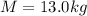
The length of the rod is
`L = 1.80 m`

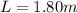
The angle the cable (string) makes with the rod is
`\theta = 80 ^o`

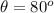
The acceleration due to gravity is
`g = 10 m/s^2`

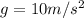
Torque is mathematically represented as

`\tau = F d \ sin \theta`

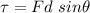
There are two torques acting on the rod

The first is torque due to gravitational force

This force is mathematically represented as

`F_g = Mg`

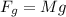
The distance is

`d = (L)/(2)`

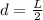
The angle is
`\theta = 90^o`

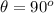
The first torque due to gravitational force

`\tau_1 = Mg * (L)/(2) * sin 90`

`\tau_1 = Mg \ (L)/(2)`

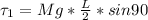
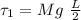
The second is torque due to the tension on the cable

The tension on the string is
`F_T`

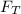
Since this force is acting at the other end of the rod , the is from that point to the point of torque(rotation ) is

`d = L`

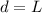
The angle which
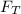`F_T` made with the point it is acting on is given as

`\thteta = 80^o`

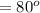
The second torque due to tension in the string is

`\tau_2 = F_T Lsin 80`

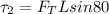
At equilibrium

`Mg \ (L)/(2) = F_T L sin 80`

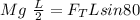
Making
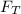`F_T` the subject of the formula we have

`F_T =( Mg )/(2 sin \ 80 )`

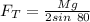
Substituting values

`F_T =( 13.0 * 10 )/(2 sin \ 80 )`

`F_T = 66 N`