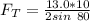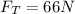Answer:
The magnitude of the tension force is
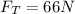
Step-by-step explanation:
The diagram of the question is shown on the first uploaded image
From the question we are told that
The mass of the rod is
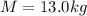
The length of the rod is

The angle the cable (string) makes with the rod is
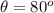
The acceleration due to gravity is
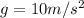
Torque is mathematically represented as
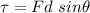
There are two torques acting on the rod
The first is torque due to gravitational force
This force is mathematically represented as
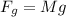
The distance is

The angle is
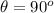
The first torque due to gravitational force

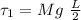
The second is torque due to the tension on the cable
The tension on the string is
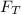
Since this force is acting at the other end of the rod , the is from that point to the point of torque(rotation ) is

The angle which
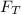 made with the point it is acting on is given as
made with the point it is acting on is given as
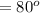
The second torque due to tension in the string is
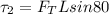
At equilibrium

Making
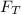 the subject of the formula we have
the subject of the formula we have
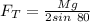
Substituting values