Question

An automobile manufacturer claims that its car has a 28.0 miles/gallon (MPG) rating. An independent testing firm has been contracted to test the MPG for this car since it is believed that the car has an incorrect manufacturer's MPG rating. After testing 270 cars, they found a mean MPG of 27.8. Assume the variance is known to be 6.25. A level of significance of 0.02 will be used. Make a decision to reject or fail to reject the null hypothesis. Make a decision.

Answer 1

The calculated value z = 1.3145 < 2.326 at 0.02 level of significance

The null hypothesis is accepted

Hence An automobile manufacturer claims that its car has a 28.0 miles/gallon (MPG) rating.

Explanation:

Step(i):-

An automobile manufacturer claims that its car has a 28.0 miles/gallon (MPG) rating.

The mean of the Population 'μ' = 28.0miles/gallon

Given data after testing 270 cars, they found a mean MPG of 27.8. Assume the variance is known to be 6.25.

The sample size 'n' = 270

Mean of the sample 'x⁻' = 27.8

Given Population variance 'σ² = 6.25

The standard deviation of Population 'σ' = √6.25 = 2.5

Step(ii):-

Null hypothesis :H₀: 'μ' = 28.

Alternative hypothesis :H₁: 'μ' ≠28.

The test statistic

`Z = (x^(-)-mean )/((S.D)/(√(n) ) )`

`Z = (27.8-28 )/((2.5)/(√(270) ) ) = (-0.2)/(0.15214)`

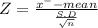
Z = -1.3145

|Z| = |-1.3145|= 1.3145

Step(iii):-

The tabulated value of z-score at 0.02 level of significance = 2.326

The calculated value z = 1.3145 < 2.326 at a t 0.02 level of significance

The null hypothesis is accepted

Hence An automobile manufacturer claims that its car has a 28.0 miles/gallon (MPG) rating.