Question

One way to measure whether the trees in the Wade Tract are uniformly distributed is to examine the average location in the north-south or the east-west direction. The values range from 0 to 200, so if the trees are uniformly distributed, the average location should be 100, and any differences in the actual sample would be due to random chance. The actual sample mean in the north-south direction for the 584 trees in the tract is 99.74. A theoretical calculation for uniform distributions (the details are beyond the scope of this course) gives a standard deviation of 58. Carefully state the null and alternative hypotheses in terms of the true average north-south location. Test your hypotheses by reporting your results along with a short summary of your conclusions.

Answer 1

Null hypothesis be H₀ : μ = 100

Alternative hypothesis Hₐ : μ < 100

There is sufficient statistical evidence to suggest that the average location of Wade Tract is 100

Explanation:

Here we have;

Let our null hypothesis be H₀ : μ = 100 Average location of trees in the Wade Tract is 100

Our alternative hypothesis becomes Hₐ : μ < 100 at 95% confidence level

Proposed average location in Wade Tract, μ = 100

Sample mean,
`\bar x` = 99.74

Standard deviation, s = 58

Sample size, n = 584

The t test formula is therefore;

`t=\frac{\bar{x}-\mu }{(s )/(√(n))}`

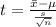
Therefore, with df = 584 -1 = 583, and α = (1 - 0.95)/2 = 0.025

We have
`t_(\alpha /2)` = -1.65

Plugging in the values into the t test formula, we have t = -0.108338, from which the p-value is given as p = 0.4569 which is much more than the value of α, therefore, we accept the null hypothesis as follows;

There is sufficient statistical evidence to suggest that the average location of Wade Tract = 100.