The equation of the hyperbola that models the sides of the drinking glass is
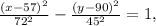 with the center at the point (57, 90).
with the center at the point (57, 90).
To derive the equation of the hyperbola, we need to consider the standard form of a hyperbola, which is
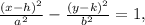 where (h, k) is the center of the hyperbola. In this scenario, the center is at the point where the diameter is minimized, which is (57, 90). The semi-major axis (a) is half of the distance between the minimum diameter points, which is
where (h, k) is the center of the hyperbola. In this scenario, the center is at the point where the diameter is minimized, which is (57, 90). The semi-major axis (a) is half of the distance between the minimum diameter points, which is
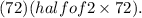 The semi-minor axis (b) is half of the height difference between the minimum and maximum diameters, which is
The semi-minor axis (b) is half of the height difference between the minimum and maximum diameters, which is
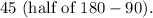
Substitute these values into the standard form equation:
![\[ ((x - 57)^2)/(72^2) - ((y - 90)^2)/(45^2) = 1. \]](https://img.qammunity.org/2021/formulas/mathematics/college/ppn46aw07lf83ulnpa5lzmjior8vtk5i69.png)
This equation models the sides of the drinking glass. The term
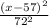 controls the horizontal shape, while
controls the horizontal shape, while
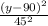 controls the vertical shape of the hyperbola. The constants (72) and (45) determine the scale of the hyperbola along the respective axes.
controls the vertical shape of the hyperbola. The constants (72) and (45) determine the scale of the hyperbola along the respective axes.
Understanding the properties of a hyperbola and its standard form allows us to model real-world shapes, such as the sides of the drinking glass. In this case, the equation accurately represents the hyperbolic shape of the glass based on the given dimensions and ensures the center corresponds to the height where the diameter is minimized.