Question

A drinking glass has sides following the shape of a hyperbola. The minimum diameter of the glass is 45 millimeters at a height of 83 millimeters. The glass has a total height of 180 millimeters, and the diameter at the top of the glass is 57 millimeters. Find the equation of a hyperbola that models the sides of the glass assuming that the center of the hyperbola occurs at the height where the diameter is minimized.

Answer 1

The equation of the hyperbola that models the sides of the drinking glass is
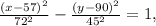`\(((x - 57)^2)/(72^2) - ((y - 90)^2)/(45^2) = 1\),` with the center at the point (57, 90).

To derive the equation of the hyperbola, we need to consider the standard form of a hyperbola, which is
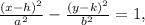`\(((x - h)^2)/(a^2) - ((y - k)^2)/(b^2) = 1\),` where (h, k) is the center of the hyperbola. In this scenario, the center is at the point where the diameter is minimized, which is (57, 90). The semi-major axis (a) is half of the distance between the minimum diameter points, which is
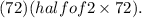`(72) (half of \(2 * 72\)).`The semi-minor axis (b) is half of the height difference between the minimum and maximum diameters, which is
`\(45\) (half of \(180 - 90\)).`

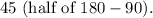
Substitute these values into the standard form equation:

`\[ ((x - 57)^2)/(72^2) - ((y - 90)^2)/(45^2) = 1. \]`

This equation models the sides of the drinking glass. The term
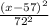`\(((x - 57)^2)/(72^2)\)` controls the horizontal shape, while
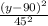`\(((y - 90)^2)/(45^2)\)` controls the vertical shape of the hyperbola. The constants (72) and (45) determine the scale of the hyperbola along the respective axes.

Understanding the properties of a hyperbola and its standard form allows us to model real-world shapes, such as the sides of the drinking glass. In this case, the equation accurately represents the hyperbolic shape of the glass based on the given dimensions and ensures the center corresponds to the height where the diameter is minimized.

Answer 2

The answer is a= 128.95 and b = 14.75

Explanation:

Solution

Given

let the equation of the hyperbola be denoted as x2/a2 - y2/b2 = 1 here, we will consider the foci on the x-axis. All units are considered to be in mm.

From question stated, with x and y coordinates represents height and radius respectively,

Then,

When x = 83 + a, y is = 45/2 = 22.5 and

At x = 180 + a, y is = 57/2 = 28.5

It is important to know that, the height is estimated from the focus so we a a is included to the heights.

Thus,

(83+a)2/a2 - 22.52/b2 = 1 and (180+a)2/a2 - 28.52/b2 = 1

By using a calculator we have, a = 128.95 and b = 14.75

Therefore a= 128.95 and b = 14.75