Answer: 3t-18
Explanation:
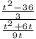
The first step is to multiply by the reciprocal of the denominator. The reciprocal of a fraction is its inverted fraction which will make it equal to 1.

This will eliminate the denominator,leaving the fraction like;
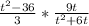
You can simplify 9 and 3;
9/3=3
3/3=1
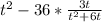
Multiply;
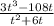
We can factor both numerator and denominator. The common factor in the numerator is 3t. And, the common factor in the denominator is t.

Now we can simplify t and t.
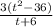
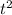 and
and
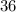 are both perfect squares with a negative (-) sign in the middle, in this case, we can extract both squares and multiply them by themselves being one positive and the other negative.
are both perfect squares with a negative (-) sign in the middle, in this case, we can extract both squares and multiply them by themselves being one positive and the other negative.
![(3[(t+6)(t-6)])/(t+6)](https://img.qammunity.org/2021/formulas/mathematics/high-school/4j478zdsp3y9nsduif5y79dwoh9xmt1xk8.png)
Since t + 6 and t - 7 are being multiplied, it is possible to simplify with the denominator. Leaving the fraction like;

Multiply;
