Answer:

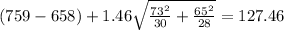
And the confidence interval for the difference of the two means is given by (74.54, 127.46)
Explanation:
Information given:
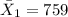 the sample mean for construction workers
the sample mean for construction workers
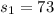 the sample standard deviation for construction workers
the sample standard deviation for construction workers
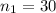 sample size of construction workers
sample size of construction workers
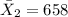 the sample mean for manufacturing workers
the sample mean for manufacturing workers
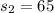 the sample standard deviation for manufacturing workers
the sample standard deviation for manufacturing workers
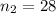 sample size of construction workers
sample size of construction workers
Confidence interval
The confidence interval for the difference of means are given by:
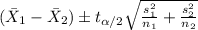
We need to find the degrees of freedom given by:

The confidence is 0.85 and the significance level would be
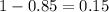 and
and
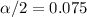 . We need to find a critical value in the t distribution who accumulates 0.075 of the area on each tail and we got:
. We need to find a critical value in the t distribution who accumulates 0.075 of the area on each tail and we got:
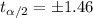
And then we can replace and we got:

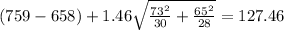
And the confidence interval for the difference of the two means is given by (74.54, 127.46)