Answer:
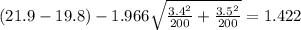
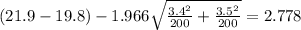
And we are 95% confident that the true difference means are between

Explanation:
We know the following info:
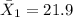 sample mean for group 1
sample mean for group 1
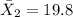 sample mean for group 2
sample mean for group 2
 sample standard deviation for group 1
sample standard deviation for group 1
 sample standard deviation for group 2
sample standard deviation for group 2
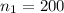 sample size group 1
sample size group 1
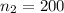 sample size group 2
sample size group 2
We want to find a confidence interval for the difference of means and the correct formula to do this is:
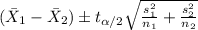
Now we just need to find the critical value. The confidence level is 0.95 then the significance is
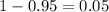 and
and
 . The degrees of freedom are given by:
. The degrees of freedom are given by:
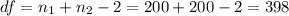
The critical value for this case would be :

And replacing into the confidence interval formula we got:
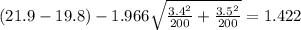
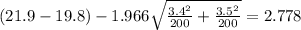
And we are 95% confident that the true difference means are between
