Question

Employees that work at a fish store must measure the level of nitrites in the water each day. Nitrite levels should remain lower than 5 ppm as to not harm the fish. The nitrite level varies according to a distribution that is approximately normal with a mean of 3 ppm. The probability that the nitrite level is less than 2 ppm is 0.0918.

Which of the following is closest to the probability that on a randomly selected day the nitrite level will be at least 5 ppm?

(A) 0.0039

(B) 0.0266

(C) 0.0918

(D) 0.7519

(E) 0.9961

Answer 1

`-1.330 = (2-3)/(\sigma)`

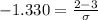
And olving for the deviation we got:

`\sigma = (2-3)/(-1.330) = 0.752`

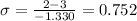
And then we want to find this probability:

`P(X>5)`

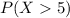
Using the z score we got:

`P(X>5)= P(Z>(5-3)/(0.752)) = P(Z>2.660)`

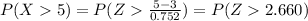
And using the complement rule and the normal standard distirbution or excel we got:

`P(X>5)= P(Z>2.660)= 1-P(Z<2.660) = 1-0.99609 =0.00391`

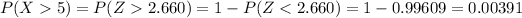
And the best answer for this case is:

(A) 0.0039

Explanation:

For this case we define the random variable X as " The nitrite level" and we know that the distribution of X is given by:

`X \sim N (\mu =3, \sigma )`

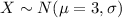
We don't know the deviation. We also know the following condition:

`P(X<2) = 0.0918`

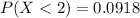
So then we can use the z score formula given by:

`z= (X -\mu)/(\sigma)`

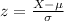
We need to find a z score value that accumulates 0.0918 of the area on the right and we got z = -1.330, since P(Z<-1.330) = 0.0918. Then we can set up the following equation:

`-1.330 = (2-3)/(\sigma)`

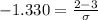
And olving for the deviation we got:

`\sigma = (2-3)/(-1.330) = 0.752`

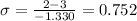
And then we want to find this probability:

`P(X>5)`

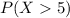
Using the z score we got:

`P(X>5)= P(Z>(5-3)/(0.752)) = P(Z>2.660)`

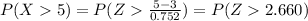
And using the complement rule and the normal standard distirbution or excel we got:

`P(X>5)= P(Z>2.660)= 1-P(Z<2.660) = 1-0.99609 =0.00391`

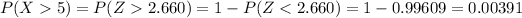
And the best answer for this case is:

(A) 0.0039