Answer:
Null hypothesis:
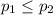
Alternative hypothesis:
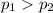
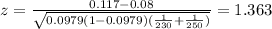
Since is a right tailed test the p value would be:
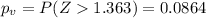
Comparing the p value and the significance level given we see that
 so then we have enough evidence to reject the null hypothesis and then the proportion of defectives for the retailer is significantly higher than the proportion of defectives for the competitor at a 10% of significance level used.
so then we have enough evidence to reject the null hypothesis and then the proportion of defectives for the retailer is significantly higher than the proportion of defectives for the competitor at a 10% of significance level used.
Explanation:
Data given
 represent the number of defectives from the retailer
represent the number of defectives from the retailer
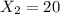 represent the number of defectives from the competitor
represent the number of defectives from the competitor
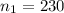 sample for the retailer
sample for the retailer
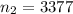 sample for the competitor
sample for the competitor
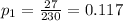 represent the proportion of defectives for the retailer
represent the proportion of defectives for the retailer
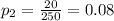 represent the proportion of defectives for the competitor
represent the proportion of defectives for the competitor
 represent the pooled estimate of p
represent the pooled estimate of p
z would represent the statistic (variable of interest)
 represent the value for the test (variable of interest)
represent the value for the test (variable of interest)
 significance level given
significance level given
System of hypothesis
We need to conduct a hypothesis in order to check if the percentage of defective cellular phones found among his products, ( p1 ), will be no higher than the percentage of defectives found in a competitor's line, ( p2 ), the system of hypothesis would be:
Null hypothesis:
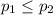
Alternative hypothesis:
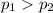
The statistic is given by:
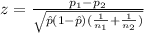 (1)
(1)
Where
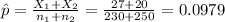
Calculate the statistic
Replacing in formula (1) the values obtained we got this:
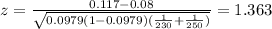
P value
Since is a right tailed test the p value would be:
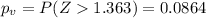
Comparing the p value and the significance level given we see that
 so then we have enough evidence to reject the null hypothesis and then the proportion of defectives for the retailer is significantly higher than the proportion of defectives for the competitor at a 10% of significance level used.
so then we have enough evidence to reject the null hypothesis and then the proportion of defectives for the retailer is significantly higher than the proportion of defectives for the competitor at a 10% of significance level used.