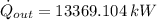Question

Steam enters a turbine operating at steady state at 2 MPa, 323 °C with a velocity of 65 m/s. Saturated vapor exits at 0.1 MPa and a velocity of 42 m/s. The elevation of the inlet is 4 m higher than at the exit. The mass flow rate of the steam is 7 kg/s, and the power developed is 8 MW. Let g = 9.81 m/s2. Determine the rate of heat transfer between the turbine and its surroundings, in kW.

Answer 1

`\dot Q_(out) = 13369.104\,kW`

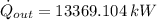
Step-by-step explanation:

The turbine is modelled after the First Law of Thermodynamics:

`-\dot Q_(out) - \dot W_(out) + \dot H_(in) - \dot H_(out) + \dot K_(in) - \dot K_(out) + \dot U_(in) - \dot U_(out) = 0`

The rate of heat transfer between the turbine and its surroundings is:

`\dot Q_(out) = \dot H_(in)-\dot H_(out) + \dot K_(in) - \dot K_(out) - \dot W_(out) + \dot U_(in) - \dot U_(out)`

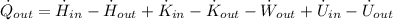
The specific enthalpies at inlet and outlet are, respectively:

`h_(in) = 3076.41\,(kJ)/(kg)`

`h_(out) = 2675.0\,(kJ)/(kg)`

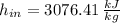
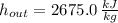
The required output is:

`\dot Q_(out) = \left(8\,(kg)/(s) \right)\cdot \left\{3076.41\,(kJ)/(kg)-2675.0\,(kJ)/(kg)+(1)/(2)\cdot \left[\left(65\,(m)/(s) \right)^(2)-\left(42\,(m)/(s) \right)^(2)\right] + \left(9.807\,(m)/(s^(2)) \right)\cdot (4\,m) \right\} - 8000\,kW`
`\dot Q_(out) = 13369.104\,kW`