Question

A 61.6 turns circular coil with radius 4.44 cm and resistance 2.34 Ω is placed in a magnetic field directed perpendicular to the plane of the coil. The magnitude of the magnetic field varies in time according to the expression B = a1 t + a2 t 2 , where a1 = 0.0411 Tsh, a2 = 0.044 M/s 2 are constants, time t is in seconds and field B is in Tesla. Find the magnitude of the induced emf in the coil at t = 9.21 s

Answer 1

Induced emf is 0.324 V

Step-by-step explanation:

We have,

Number of turns, n = 61.6

Radius of circular coil, r = 4.44 cm

Resistance of coil, R = 2.34 Ω

The magnitude of the magnetic field varies in time according to the expression :

`B=a_1t+a_2t^2`

`a_1=0.0411\\\\a_2=0.044`

The magnitude of the induced emf in the coil is given by :

`\epsilon=(d\phi)/(dt)\\\\\epsilon=(d(NBA))/(dt)\\\\\epsilon=NA(dB)/(dt)`

`\epsilon=\pi r^2(dB)/(dt)`

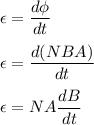
At t = 9.21 s,

`(dB)/(dt)=(0.0411+2* 0.044 * 9.21)\\\\(dB)/(dt)=0.851\ T/s`

`\epsilon=61.6* \pi * (4.44 * 10^(-2))^2* 0.851`

`\epsilon=5.27* 10^(-3)\ V`

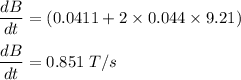
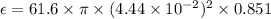
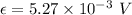
So, the magnitude of the induced emf in the coil is 0.324 V