Answer:
Induced emf is 0.324 V
Step-by-step explanation:
We have,
Number of turns, n = 61.6
Radius of circular coil, r = 4.44 cm
Resistance of coil, R = 2.34 Ω
The magnitude of the magnetic field varies in time according to the expression :
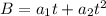
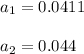
The magnitude of the induced emf in the coil is given by :
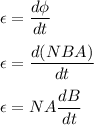
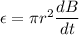
At t = 9.21 s,
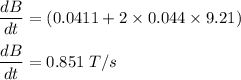
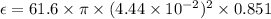
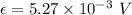
So, the magnitude of the induced emf in the coil is 0.324 V