Question

5. A gas occupies 2000. L at 100.0 K and exerts a pressure of 100.0 kPa. What volume will the gas occupy if the temperature is increased to 400. K and the pressure is increased to 200. kPa?

Answer 1

The volume that the gas will occupy when the temperature is increased to 400.0 K and the pressure is increased to 200. kPa is 4000. L

Step-by-step explanation:

Here we are required to utilize the combined gas equation as follows;

`(P_(1)* V_(1))/(T_(1)) = (P_(2)* V_(2))/(T_(2))`

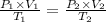
Where:

P₁ = Initial pressure of the gas = 100.0 kPa

V₁ = Initial volume of the gas = 2000. L

T₁ = Initial temperature of the gas = 100.0 K

P₂ = Final pressure of the gas = 200.0 kPa

V₂ = Final volume of the gas = Required

T₂ = Final temperature of the gas = 400.0 K

Making V₂ the formula subject of the combined gas equation, we have;

`V_(2)}{} = (P_(1)* V_(1)* T_(2) )/(T_(1)* P_(2))`

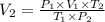
Therefore, by plugging the values, we have;

`V_(2)}{} = (100.0* 2000* 400.0 )/(100.0 * 200.0 ) = 4000. \, L`

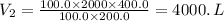
The volume that the gas will occupy when the temperature is increased to 400.0 K and the pressure is increased to 200. kPa = 4000. L.

Answer 2

The gas will occupy a volume of 4000L

Step-by-step explanation:

V1 = 2000L

T1 = 100K

P1 = 100kPa = 100*10³Pa

T2 = 400k

P2 = 200kPa = 200*10³kPa

V2 = ?

To solve this question, we need to use combined gas equation

[(P₁ * V₁) / T₁] = [(P₂ * V₂) / T₂]

V₂ = (P₁ * V₁ * T₂) / (P₂ * T₁)

V₂ = (100*10³ * 2000 * 400) / (200*10³ * 100)

V₂ = 8.0*10¹⁰ / 2.0*10⁷

V₂ = 4000L

The new volume of the gas is 4000L