Answer:
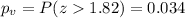
Assuming a standard significance level of
 the best conclusion for this case would be:
the best conclusion for this case would be:
4. There is not enough evidence to show that more than 35% of community college students own a smart phone (P-value = 0.034).
Because

If we select a significance level lower than 0.034 then the conclusion would change.
Explanation:
Data given
n=300 represent the random sample taken
X=120 represent the people who have a smart phone
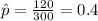 estimated proportion of people who have a smart phone
estimated proportion of people who have a smart phone
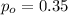 is the value that we want to test
is the value that we want to test
z would represent the statistic (variable of interest)
 represent the p value (variable of interest)
represent the p value (variable of interest)
System of hypothesis
We need to conduct a hypothesis in order to test the claim that the true proportion of people who have a smart phone is higher than 0.35, the system of hypothesis are.:
Null hypothesis:
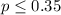
Alternative hypothesis:

The statistic is given by:
 (1)
(1)
Calculate the statistic
Since we have all the info requires we can replace in formula (1) like this:
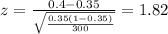
Statistical decision
Since is a right tailed test the p value would be:
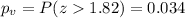
Assuming a standard significance level of
 the best conclusion for this case would be:
the best conclusion for this case would be:
4. There is not enough evidence to show that more than 35% of community college students own a smart phone (P-value = 0.034).
Because

If we select a significance level lower than 0.034 then the conclusion would change.