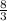Answer:
x =
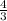 , x =
, x =
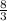
Explanation:
Given
- 2 | 3x - 6 | + 5 = 1 ( subtract 5 from both sides )
- 2 | 3x - 6 | = - 4 ( divide both sides by - 2 )
| 3x - 6 | = 2
The absolute value function always returns a positive solution, however, the expression inside can be positive or negative, that is
3x - 6 = 2 ( add 6 to both sides )
3x = 8 ( divide both sides by 3 )
x =
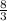
OR
- (3x - 6) = 2, that is
- 3x + 6 = 2 ( subtract 6 from both sides )
- 3x = - 4 ( divide both sides by - 3 )
x =
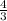
As a check
Substitute these values into the left side of the equation and if equal to the right side then they are the solutions.
x =
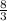 : - 2| 8 - 6 | + 5 = - 2| 2| + 5 = -2(2) + 5 = - 4 + 5 = 1 = right side
: - 2| 8 - 6 | + 5 = - 2| 2| + 5 = -2(2) + 5 = - 4 + 5 = 1 = right side
x =
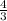 : - 2 | 4 - 6| + 5 = - 2| - 2| + 5 = - 2(2) + 5 = - 4 + 5 = 1 = right side
: - 2 | 4 - 6| + 5 = - 2| - 2| + 5 = - 2(2) + 5 = - 4 + 5 = 1 = right side
Thus the solutions are x =
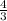 and x =
and x =