Answer:
W = 54.6 MJ ... ( 3 sig fig )
Step-by-step explanation:
Given:-
- The thermal conductivity of wall, k = 0.35 W/m°C
- The thickness of wall , L = 16 cm
- The surface dimension of wall A = ( 2.7 x 6 ) m
- The time duration t = 18.6 hours
- The inside temperature, Ti = 31°C
- The outside temperature, To = 8°C
Find:-
How much heat flows through the wall in a 18.6 h period
Solution:-
- The Fourier's law of heat conduction in ( one - dimension ) through any material with thermal conductivity "k" is represented by the rate of heat transfer in the direction of x.
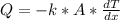
- The fully derived expression for conduction heat transfer is given by:

- Plug in the given values and compute the rate of heat transfer:
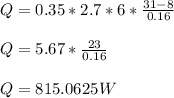
- The heat energy that flows through the wall during time t = 18.6 hrs is given by W:
W = Q*t*3600 / 10^6
W = 815.0625*18.6*3600 / 10^6
W = 54576585 / 10^6 MJ
W = 54.6 MJ ... ( 3 sig fig )