Question

A circle with the equation (x + 4)2 + (y + 2)2 = 36 is reflected over the line x = 1. What is the equation of the image? (x + 4)2 + (y - 2)2 = 36 (x - 6)2 + (y + 2)2 = 36 (x + 6)2 + (y - 2)2 = 36 (x - 4)2 + (y + 2)2 = 36

Answer 1

(x - 6)² + (y + 2)² = 36

Explanation:

Centre before reflection: (-4,-2)

Centre after reflection:

(-4+5+5,-2) = (6,-2)

(x - 6)² + (y + 2)² = 36

Answer 2

B

Explanation:

Currently, the graph looks like the attachment.

The centre of this circle is at (-4, -2), but when we flip it over the line x = 1 (the blue line on the picture), the centre will become ((1- -4) + 1, -2) = (6, -2).

Look for the equation
`(x-h)^2+(y-k)^2=r^2` that matches this center. We want the center (h, k) to be (6, -2), so our equation should look something like:

`(x-6)^2+(y+2)^2=36`

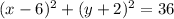
The answer is B.