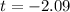Question

An engineer has designed a valve that will regulate water pressure on an automobile engine. The valve was tested on 280 engines and the mean pressure was 6.5

pounds/square inch (psi). Assume the population variance is 0.64. The engineer designed the valve such that it would produce a mean pressure of 6.6 psi. It is believed
that the valve does not perform to the specifications. A level of significance of 0.02 will be used. Find the value of the test statistic. Round your answer to two decimal
places

Answer 1

The value of the test statistic is
`t = -2.09`

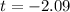
Explanation:

The null hypothesis is:

`H_(0) = 6.6`

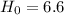
The alternate hypotesis is:

`H_(1) \\eq 6.6`

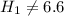
Our test statistic is:

`t = (X - \mu)/((\sigma)/(√(n)))`

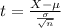
In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`\sigma` is the standard deviation(square roof of the variance) and n is the size of the sample.

In this problem, we have that:

`X = 6.5, \mu = 6.6, \sigma = √(0.64) = 0.8, n = 280`

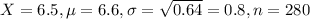
So

`t = (X - \mu)/((\sigma)/(√(n)))`

`t = (6.5 - 6.6)/((0.8)/(√(280)))`

`t = -2.09`

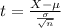
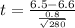
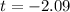
The value of the test statistic is
`t = -2.09`