Question

Write the equation of a line in slope-intercept form that goes through the points

(4, -2) and (-4, -4).

A.
y = 1/4x - 3
B.
y = 4x - 3

C.
y = 4x - 2

d
y = 1/4x - 2

Answer 1

Slope-intercept form: y = mx + b

(m is the slope, b is the y-intercept or the y value when x = 0 --> (0, y) or the point where the line crosses through the y-axis)

To find the slope(m), use the slope formula:

`m=(y_2-y_1)/(x_2-x_1)` And plug in the two points on the line

(-4, -4) = (x₁, y₁)

(4, -2) = (x₂, y₂)

`m=(y_2-y_1)/(x_2-x_1)`

`m=(-2-(-4))/(4-(-4))` (two negative signs cancel each other out and become positive)

`m=(-2+4)/(4+4)`

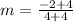
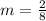`m=(2)/(8)` Simplify the fraction

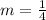`m=(1)/(4)` Now that you know the slope, substitute/plug it into the equation

y = mx + b

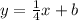`y=(1)/(4) x+b` To find b, plug in either of the points into the equation, it doesn't matter which, then isolate/get the variable "b" by itself. I will use (4, -2)

`-2=(1)/(4)(4)+b`

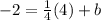
-2 = 1 + b Subtract 1 on both sides to get "b" by itself

-3 = b

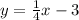`y=(1)/(4) x-3` Your answer is A