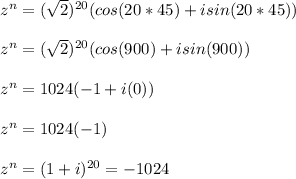Answer:
-1024
Explanation:
Moivre's theorem allows to easily obtain trigonometric formulas that express the sine and cosine of a multiple angle as a function of the sine and cosine of a simple angle.
De Moivre's theorem can be applied to any complex number

Where:
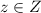
Let:
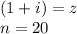
According to Demoivres Theorem, If:
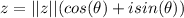
Then:
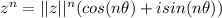
For a complex number
 :
:
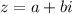
Its magnitude and angle are given by:
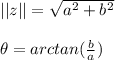
So:
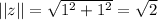
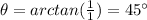
Therefore, using De Moivre's theorem: