Question

If the diagonal of a square is approximately 12.73, what is the length of its sides?

Answer 1

The length of the sides of the square is 9.0015

Explanation:

Given

The diagonal of a square = 12.73

Required

The length of its side

Let the length and the diagonal of the square be represented by L and D, respectively.

So that

D = 12.73

The relationship between the diagonal and the length of a square is given by the Pythagoras theorem as follows:

`D^(2) = L^(2) + L^(2)`

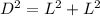
Solving further, we have

`D^(2) = 2L^(2)`

Divide both sides by 2

`(D^(2))/(2) = (2L^(2))/(2)`

`(D^(2))/(2) = L^2`

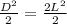
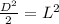
Take Square root of both sides

`\sqrt{(D^(2))/(2)} = √(L^2)`

`\sqrt{(D^(2))/(2)} = L`

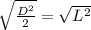
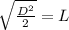
Reorder

`L = \sqrt{(D^(2))/(2)}`

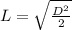
Now, the value of L can be calculated by substituting 12.73 for D

`L = \sqrt{(12.73^(2))/(2)}`

`L = \sqrt{(162.0529)/(2)}`

`L = \sqrt{{81.02645}`

`L = 9.001469325`

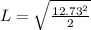
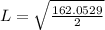
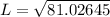
`L = 9.0015` (Approximated)

Hence, the length of the sides of the square is approximately 9.0015