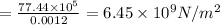Answer:
(A) Strain = 0.0012
(b) Stress
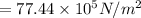
(c) Young's modulus
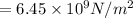
Step-by-step explanation:
Mass of the rock m = 75 kg
So weight of the rock
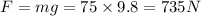
Length of the rope l = 18 m
Diameter of the rope d = 11 mm
Change in length of rope

So radius r = 5.5 mm = 0.0055 m
Cross sectional area
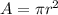
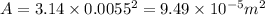
(a) Strain is equal to ratio change in length to original length
So strain

(b) Stress
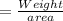

(c) Young's modulus is equal to ratio of stress and strain
So young's modulus