Question

Points and their residual values are shown in the table. A 3-column table with 5 rows. The first column is labeled x with entries 1, 2, 3, 4, 5. The second column is labeled y with entries 2, 3.5, 5, 6.1, 8. The third column is labeled residual value with entries negative 0.4, 0.7, negative 0.2, negative 0.6. Which residual value is the farthest from the line of best fit?

Answer 1

the answer is 0.7

Step-by-step explanation: its simple the higher the value is the farther the pint is from the line of best fit.

Answer 2

The residual value is the farthest from the line of best fit is 0.7.

Explanation:

A simple linear regression line is given by,

`\hat y = \alpha + \beta X + \hat e`

Here,

α = constant,

β = slope

e = residual.

The difference amid the observed value of the dependent variable (Y) and the predicted value (y) is known as the residual (e).

The formula to compute the residual is,

`\hat e=y-\hat y`

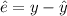
The information provided is:

x y e

1 2.0 -0.4

2 3.5 0.7

3 5.0 -0.2

4 6.1 -0.6

5 8.0 0.0

The residuals are the difference between the actual value and the predicted value.

They can also be defined as the distance between the line of best fit and the actual value of the dependent variable.

The data point that is the farthest from the line of best fit is, y = 3.5.

The residual value of y = 3.5 is 0.7.

In terms of units distance, this value of y is the farthest from the line of bet fit.

Thus, the residual value is the farthest from the line of best fit is 0.7.