Answer:
A function can be described as one-to-one or many-to-one, i.e. each value in the domain (
 -values) is mapped to a single value in f(x).
-values) is mapped to a single value in f(x).
An example of a one-to-one function is a linear function. For every value of x there is one value of y.
An example of a many-to-one function is a quadratic function, where 2 different x-values map to one y-value.
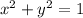 is not a function as some values of
is not a function as some values of
 are mapped to two different values of f(x).
are mapped to two different values of f(x).
For example, let x = 0.5
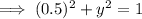

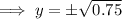
So as x = 0.5 maps to √0.75 and -√0.75, it is one-to-many, and is therefore not a function.