Question

6.3.6. Among the early attempts to revisit the death postponement theory introduced in Case Study 6.3.2 was an examination of the birth dates and death dates of three hundred forty-eight U.S. celebrities (144). It was found that sixteen of those individuals had died in the month preceding their birth month. Set up and test the appropriate H0 against a one-sided H1. Use the 0.05 level of significance.

Answer 1

The question involves statistical hypothesis testing where the null hypothesis (H0) suggests no significant increase in celebrity deaths before their birth month, and the alternative hypothesis (H1) suggests a significant increase. Using significance level 0.05 and the provided data, the p-value is compared to decide on H0.

Step-by-step explanation:

The question provided relates to setting up and testing a null hypothesis (H0) against a one-sided alternative hypothesis (H1) in the context of statistical hypothesis testing. Specifically, it involves determining whether the occurrence of celebrity deaths in the month preceding their birth month is statistically significant using a significance level of 0.05. To address this, the null hypothesis would state that there is no significant increase in the frequency of deaths in the month before the celebrities' birth month compared to any other month. The alternative hypothesis would state that there is a significant increase in deaths in the month preceding the birth month of celebrities. We would use the data provided (16 out of 348 celebrities dying in the month before their birth month) to calculate the p-value and compare it with the alpha level of 0.05 to decide whether to reject the null hypothesis or not.

Answer 2

So the Null hypothesis is rejected in this case

Step-by-step explanation:

The number of celebrities is n = 348

So to solve this we would assume that p is the percentage of people that died on the month preceding their birth month

Generally if there is no death postponement then p will be mathematically evaluated as

`p = (1)/(12)`

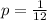
This implies the probability of date in one month out of the 12 months

Now from the question we can deduce that the hypothesis we are going to be testing is

`Null Hypothesis \ \ H_0 : p = 0.083`

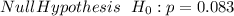
This is a hypothesis is stating that a celebrity dies in the month preceding their birth

`Alternative \ Hypothesis H_1 : p < 0.083`

This is a hypothesis is stating that a celebrity does not die in the month preceding their birth

is c is the represent probability for each celebrity which either c = 0 or c = 1

Where c = 0 is that the probability that the celebrity does not die on the month preceding his/ her birth month

and c = 1 is that the probability that the celebrity dies on the month preceding his/ her birth month

Then it implies that

for

n= 1 + 2 + 3 + .... + 348 celebrities

Then the sum of c for each celebrity would be
`c_s = 16`

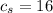
i.e The number of celebrities that died in the month preceding their birth month

We are told that the significance level is
`\alpha = 0.05`, the the z value of
`\alpha` is

`z_(\alpha ) = 1.65`

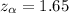
This is obtained from the z-table

Since this test is carried out on the left side of the area under the normal curve then the critical value will be

`z_(\alpha ) = - 1.65`

So what this implies is that
`H_o` will be rejected if

`z \le -1.65`

Here z is the test statistics

Now z is mathematically evaluated as follows

`z = (c - np)/(√(np_o(1- p_o)) )`

`z = (16 - (348 *0.083))/(√(348*0.083 (1- 0.083)) )`

`z =-2.50`

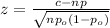
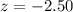
From our calculation we see that the value of z is less than
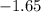`-1.65` so the Null hypothesis will be rejected

Hence this tell us that the evidence provided is not enough to conclude that 16 celebrities died a month to their birth month