Question

3. The length of a rectangle is increasing at a rate of 3 cm=s and its width is increasing at arate of 9 cm=s. When the length is 7 cm and the width is 5 cm, how fast is the area of therectangle increasing?

Answer 1

`(dA)/(dt) = 78cm/sec`

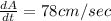
The area of the rectangle is increasing at 78cm/sec

Explanation:

Explanation:-

Given the length of a rectangle is increasing at a rate of 3 cm/s

`(dl)/(dt) = 3cm/s`

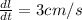
Given the width of a rectangle is increasing at a rate of 9 cm/s

`(dw)/(dt) = 9cm/s`

we know that the area of the rectangle

A = l × w …(l)

Differentiating equation with respective to 't'

`(dA)/(dt) = l ((dw)/(dt) )+ w ((dl)/(dt) )`

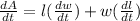
Given the length of the rectangle = 7 cm and

The width of the rectangle w = 5 cm

`(dA)/(dt) = 7(9)+5(3) = 78`

`(dA)/(dt) = 78cm/sec`

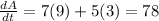
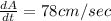
Final answer:-

The area of the rectangle is increasing at 78cm/sec