Answer:
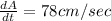
The area of the rectangle is increasing at 78cm/sec
Explanation:
Explanation:-
Given the length of a rectangle is increasing at a rate of 3 cm/s
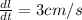
Given the width of a rectangle is increasing at a rate of 9 cm/s
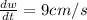
we know that the area of the rectangle
A = l × w …(l)
Differentiating equation with respective to 't'
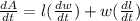
Given the length of the rectangle = 7 cm and
The width of the rectangle w = 5 cm
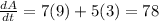
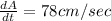
Final answer:-
The area of the rectangle is increasing at 78cm/sec