Answer:
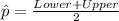
And replacing the info from the problem we have:
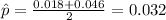
So then the best estimator for the true proportion p is given by
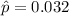 or equivalent to 3.2 %
or equivalent to 3.2 %
Explanation:
We want to find a confidence interval for a proportion p who represent the parameter of interest.
The confidence interval would be given by this formula:
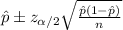
For this case the 90% confidence interval is given by (1.8%=0.018, 4.6%=0.046) after apply the last formula
Since the confidence interval is symmetrical we can estimate the point estimator of the true percentage with this formula:
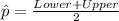
And replacing the info from the problem we have:
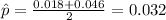
So then the best estimator for the true proportion p is given by
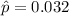 or equivalent to 3.2 %
or equivalent to 3.2 %